fairness, equal odds postprocessing
Orange Fairness - Equal Odds Postprocessing
Žan Mervič
Sep 19, 2023
In the previous blog post, we discussed the Adversarial Debiasing model, a bias-aware model. This blog post will discuss the Equal Odds Postprocessing widget, a bias-aware post-processor, which can be used with any model to mitigate bias in its predictions.
Equal Odds Postprocessing:
The Equal Odds Postprocessing widget is a post-processing type of fairness mitigation algorithm for supervised learning. It modifies the predictions of any given classifier to meet certain fairness criteria, specifically focusing on "Equalized Odds" or more relaxed criteria like Equal Opportunity. Because it is a post-processing algorithm, it is versatile and can be used with most models, unlike some pre-processing or in-processing algorithms.
The Equalized Odds Postprocessing widget introduces a unique functionality in the Orange environment. It works similarly to other Orange widgets representing models, except it also expects a learner as an input.
It works by first fitting the learner to the training data, creating a model, and using it to get the predictions. It then uses these predictions to fit the Equalized Odds Postprocessing algorithm from the AIF360 library, which creates a post-processor. This post-processor is then used to adjust the model's predictions on the test data. The result is a model that has been adjusted to meet the fairness criteria of Equalized Odds.
The Equalized Odds Postprocessing algorithm works by solving a linear program with some constraints and the following objective function:
c = [fpr_0 - tpr_0, tnr_0 - fnr_0, fpr_1 - tpr_1, tnr_1 - fnr_1]
Where fpr, tpr, tnr, and fnr are the false positive, true positive, true negative, and false negative rates for privileged (0) and unprivileged (1) groups.
The algorithm then finds the optimal solution to the linear program, which results in a set of probabilities with which to flip the model's predictions to equalize the odds of being correctly or incorrectly classified for both privileged and unprivileged groups:
sp2p: From positive to negative for the privileged group.sn2p: From negative to positive for the privileged group.op2p: From positive to negative for the unprivileged group.on2p: From negative to positive for the unprivileged group.
Orange use case
Now that we know how the Equal Odds Postprocessing widget works and how to use it let us look at a real-world example for a classification task.
For this example, we will use the German credit dataset, which we have used before. The German Credit is a dataset related to bank loans. The main goal is to assess an individual's credit risk - whether a person is a good or bad credit risk. Unlike previously, we will not use the default fairness attributes that come with the dataset. Instead, we will use the age attribute, which we first discretize to two groups, younger and older than 26. We will set the older group as the privileged group.
We will train two Logistic Regression models, one with and one without the Equal Odds Postprocessing widget, and compare the predictions of these models.
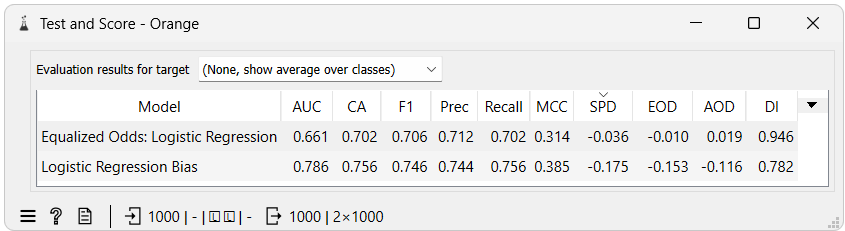
The results show that the model using the Equal Odds Postprocessing widget has better fairness metrics than the model without it. Equal Odds Difference and Average Odds Difference are the main objectives of the Equal Odds Postprocessing algorithm, and we can see that they are much closer to zero when using the widget. We can also see that the Disparate Impact and Statistical Parity Difference metrics are much closer to their ideal values, which is a beneficial side effect rather than a direct result of the algorithm's optimization process and is not guaranteed to happen in all cases.
We can also see that the model's accuracy using the Equal Odds Postprocessing widget is slightly lower than without it. This is expected because the model is now not only trying to be accurate but also fair. This balance is a necessary trade-off we accept when we want to remove bias.
When using the Equal Odds Postprocessing, it is worth noting that the AUC value is not an accurate representation of the model's performance. This is because the Equal Odds Postprocessing algorithm changes only the predictions of the model, not the prediction probabilities. This means the AUC value would be calculated from the original model's prediction probabilities, not the adjusted ones. We have decided to alter the prediction probabilities when using the Equal Odds Postprocessing widget to 1 if the prediction is of the positive class and 0 otherwise. This is done to ensure that the AUC value is calculated from the adjusted predictions, which is a more accurate representation of the model's performance but still not a perfect one.
Next, let us look at the box-plot widget. We will use it to show the True Positive Rate for each group and thus the Equal Opportunity Difference metric, which is the difference of the True Positive Rates between unprivileged and privileged groups. To do this, we first had to use the Select Rows widget to keep only the instances with a positive class because we are not interested in the True/False Negative Rate. This was the result:
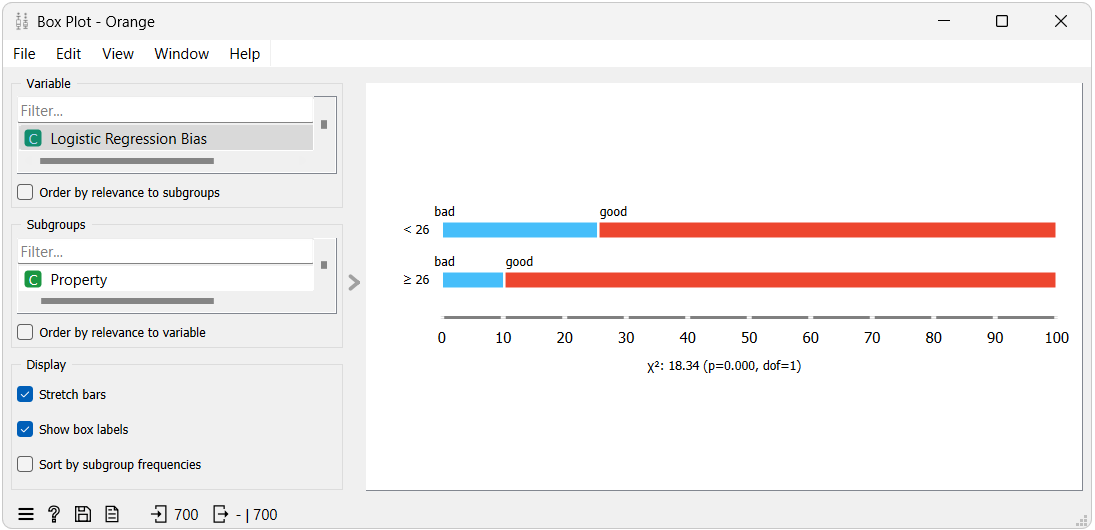
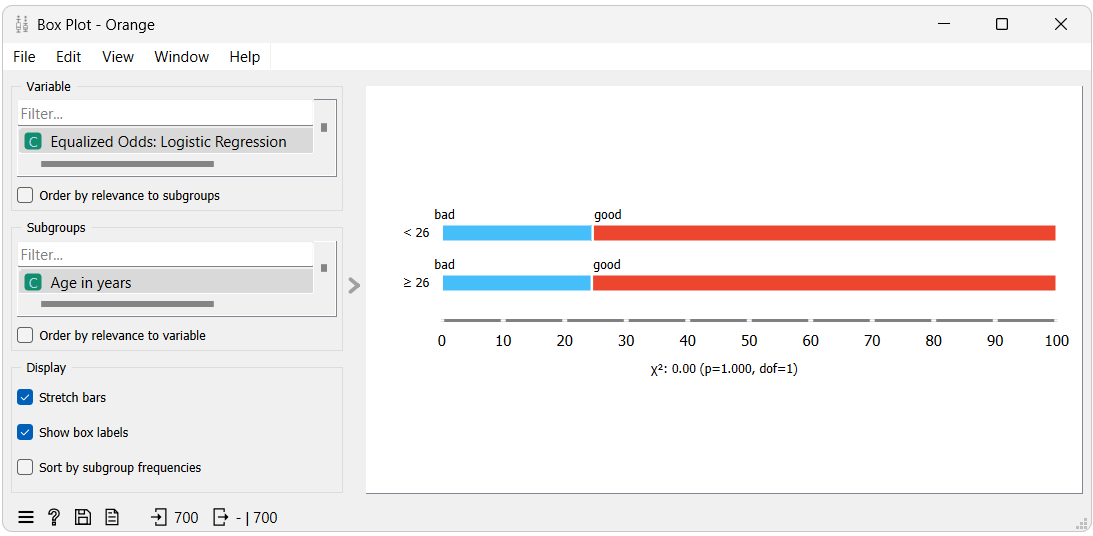
In the visualizations, each rows's red and blue parts represent the true positive and false negative rates, respectively, for each group.
In the first visualization, which represents predictions from the model without debiasing, we can see that the privileged group (≥ 26) has a higher True Positive Rate than the unprivileged group (< 26). This can be considered unfair towards the unprivileged group because it means a loan candidate from the unprivileged group is more likely to be falsely rejected, because of the higher false negative rate, than a loan candidate from the privileged group.
In the second visualization, representing predictions from the model with debiasing, we can see that the True Positive Rate for the privileged group has decreased and is now almost equal to the True Positive Rate for the unprivileged group. While this means the model is now less accurate for the privileged group, it is as accurate as it is for the unprivileged group, which could be considered a fairer outcome.